Wind Loads: Explained in 1-minute

Wind Loading is not taught in great detail at most universities but it is an important design factor for the design of a buildings lateral force resisting systems. Hopefully this article can help shed some slight on the very basic aspects of wind loading.

Wind Pressure on Buildings

When wind blows over a building, there are areas of low pressure (suction, air moving away from the surface i.e. negative pressure) and high pressure (overpressure, air moving towards the surface i.e. positive pressure).

An example for wind on a house is shown below:

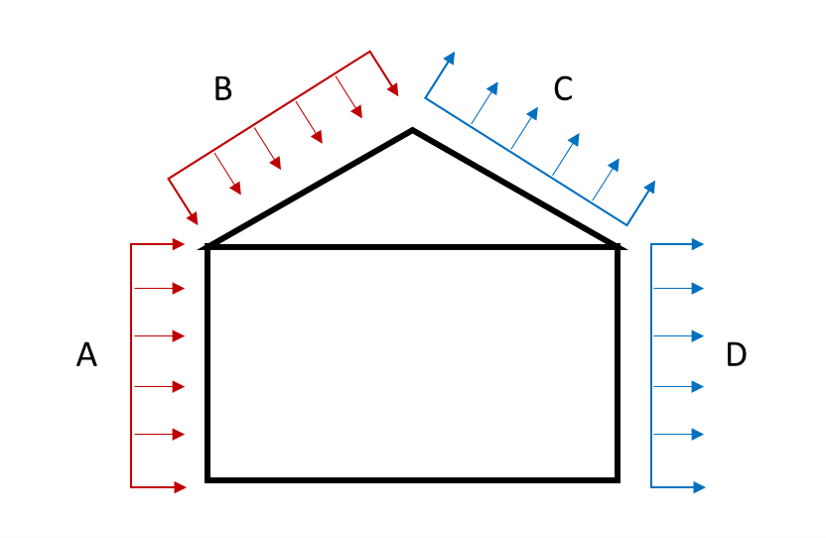The wind pressure on surface A, is a uniformly distributed pressure, expressed in kN/m2 or N/mm2.

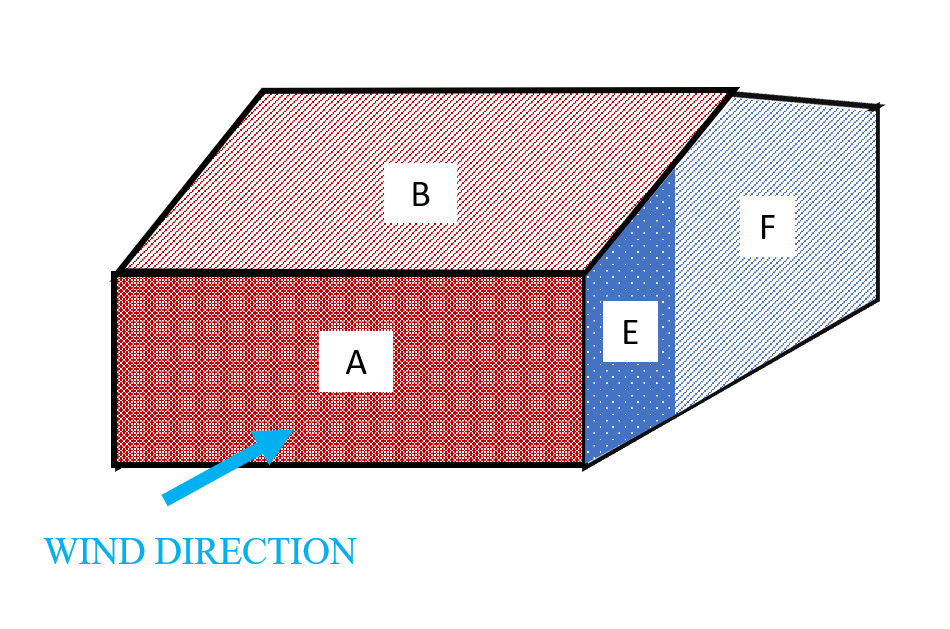
A simplified 3d example is shown below, with colours representing the pressure magnitudes (darker colours indicate higher magnitudes). Of course the real pressure variation is much more sophisticated.

The site-specific wind pressure represents the maximum pressure corresponding to a short gust duration (typically a 1- to 3 second gust) in free flowing wind conditions. It can be calculated by using the following equation:

Wind Pressure,

ρ is the air pressure, generally taken as 1.225 kg/m3 and U is the Wind Speed (usually at a reference height such as the top of the building).

By multiplying the site wind pressure by a pressure coefficient, one can obtain local (cladding) or overall (structural) wind pressures to apply to the building.

Cp,net is the net pressure coefficient and is defined as follows:

Net Pressure Coefficient,

Where Cpe and Cpi are the external and internal pressure coefficients, respectively. These values are widely available in building codes for different building shapes and pressure regions.

※ How to obtain the external pressure coefficient for wind loading?

※ How to obtain the internal pressure coefficient for wind loading?

In reality, the wind pressures varies over the full height of the building, following the shape of the site-specific wind speed profile. For more information on deriving the wind speed and wind pressure profile, refer to the articles below.

※ How to obtain the wind speed pressure profile? Eurocode approach

Wind Force on Buildings 

Knowing the structural/cladding wind pressures, we can calculate the force acting on an area as follows:

Overall Structural Wind Force,

Where P is the pressure and A is the tributary area.

※ What is the tributary area for wind loading? Explained in 1-minute.

For tall buildings, the wind pressure varies with height, so the wind force can be calculated on a storey-by-storey basis. In this case, the tributary heights for each storey can be considered as half the distance to the storeys above and below... as shown in the image below.

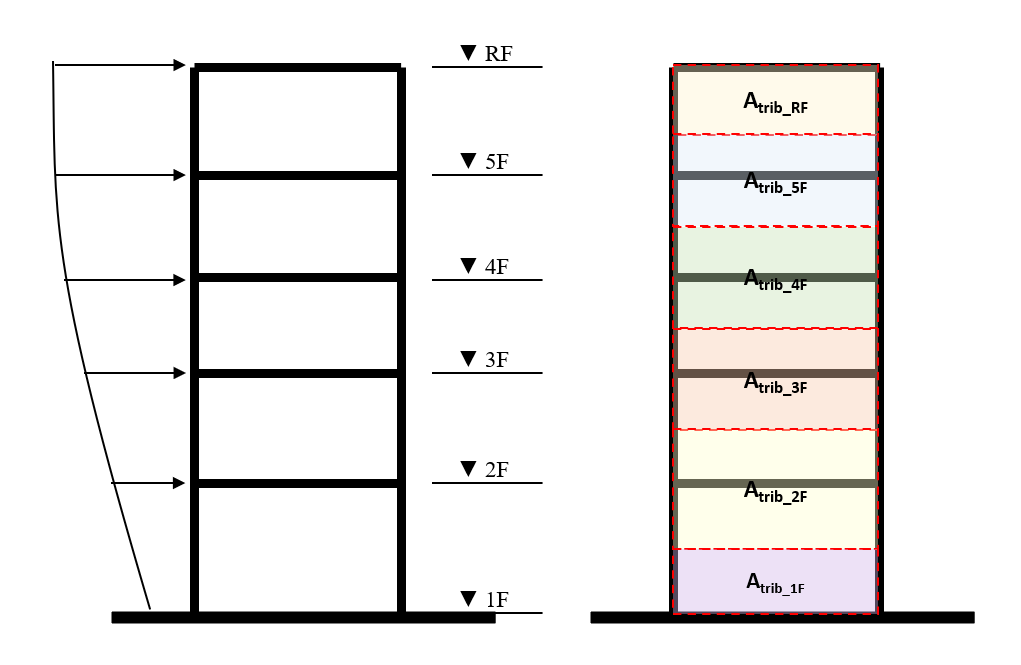
Example Calculation for Tall Building

Consider a tall building which is 30 m x 45 m in plan, and 180 m tall. The calculated site wind pressure at the top of the building is found to be 1.50 kN/m2. Calculate the overall wind force and overturning moment for wind to the front of the building (projected width of 30 m).